Optimizing a Fantasy Football Squad with OR-Tools and .NET

Introduction

While building my fantasy football site xperty.se, I wanted to add a tool that automatically picks the best possible team within a set of strict constraints. This post walks through how I implemented an optimizer using C# and Google’s OR-Tools to create the optimal squad for fantasy football.

1. The Problem

Fantasy football isn’t just about picking your favorite players. You’re limited by:

• A budget cap
• A fixed number of players per position
• A max of 3 players per real-life team

I wanted to automate the selection process to find the team with the highest expected points while staying within these limits.

2. The Tools

• .NET (C#): For the core application logic
• Google OR-Tools: For solving the optimization problem

3. Modeling the Squad Selection as an Optimization Problem

We treat this as a Mixed Integer Linear Programming problem. Each player is represented by a boolean variable – either they’re in the squad or not.

🎯 Objective Function: Maximize Expected Points

objective.SetCoefficient(playerVars[player.Name], player.ExpectedPoints);
objective.SetMaximization();

💰 Constraint: Stay Under Budget

Constraint budgetConstraint = solver.MakeConstraint(0, (double)budget);
budgetConstraint.SetCoefficient(playerVars[player.Name], (double)player.Cost);

📌 Position Constraints

Constraint midfieldersConstraint = solver.MakeConstraint(5, 5);
midfieldersConstraint.SetCoefficient(playerVars[player.Name], 1);

🛑 Max 3 Players Per Team

Constraint teamConstraint = solver.MakeConstraint(0, 3);
teamConstraint.SetCoefficient(playerVars[player.Name], 1);

4. The Code

Here’s a more detailed version of the core logic:

public static class SquadSelector
{
    // Define the team constraints
    private const int MaxPlayersPerTeam = 3;
    private const int NumGoalkeepers = 2;
    private const int NumDefenders = 5;
    private const int NumMidfielders = 5;
    private const int NumForwards = 3;

    public static FantasySquad OptimizeTeam(List<SquadPlayer> players)
    {
        var budget = 100M;

        var selectedPlayers = new List<SquadPlayer>();

        // Create the solver
        var solver = Solver.CreateSolver("SCIP");

        // Define the decision variables
        Dictionary<string, Variable> playerVars = [];

        foreach (var player in players)
        {
            playerVars[player.Name] = solver.MakeBoolVar(player.Name);
        }

        // Define the objective function
        var objective = solver.Objective();
        objective.SetMaximization();

        foreach (var player in players)
        {
            objective.SetCoefficient(playerVars[player.Name], player.ExpectedPoints);
        }

        // Add the budget constraint
        Constraint budgetConstraint = solver.MakeConstraint(0, (double)budget);

        foreach (var player in players)
        {
            budgetConstraint.SetCoefficient(playerVars[player.Name], (double)player.Cost);
        }

        // Add the position constraints
        Constraint goalkeepersConstraint = solver.MakeConstraint(NumGoalkeepers, NumGoalkeepers);
        Constraint defendersConstraint = solver.MakeConstraint(NumDefenders, NumDefenders);
        Constraint midfieldersConstraint = solver.MakeConstraint(NumMidfielders, NumMidfielders);
        Constraint forwardsConstraint = solver.MakeConstraint(NumForwards, NumForwards);

        foreach (var player in players)
        {
            if (player.PlayerType == 1)
            {
                goalkeepersConstraint.SetCoefficient(playerVars[player.Name], 1);
            }
            else if (player.PlayerType == 2)
            {
                defendersConstraint.SetCoefficient(playerVars[player.Name], 1);
            }
            else if (player.PlayerType == 3)
            {
                midfieldersConstraint.SetCoefficient(playerVars[player.Name], 1);
            }
            else if (player.PlayerType == 4)
            {
                forwardsConstraint.SetCoefficient(playerVars[player.Name], 1);
            }
        }

        // Add the constraint for maximum players per team
        var teams = players.Select(p => p.TeamId).Distinct();

        foreach (var team in teams)
        {
            Constraint teamConstraint = solver.MakeConstraint(0, MaxPlayersPerTeam, $"MaxPlayersPerTeam_{team}");

            foreach (var player in players.Where(p => p.TeamId == team))
            {
                teamConstraint.SetCoefficient(playerVars[player.Name], 1);
            }
        }

        // Solve the problem
        Solver.ResultStatus resultStatus = solver.Solve();

        // Get the selected players
        foreach (var player in players)
        {
            if (playerVars[player.Name].SolutionValue() > 0.5)
            {
                selectedPlayers.Add(player);
            }
        }

        // Release resources
        solver.Dispose();

        ...
}

5. Real-World Application on Xperty

This logic is now live and powers the auto-pick functionality on xperty.se. Users can click one button and get the best possible team based on latest projections – no manual tweaking required.

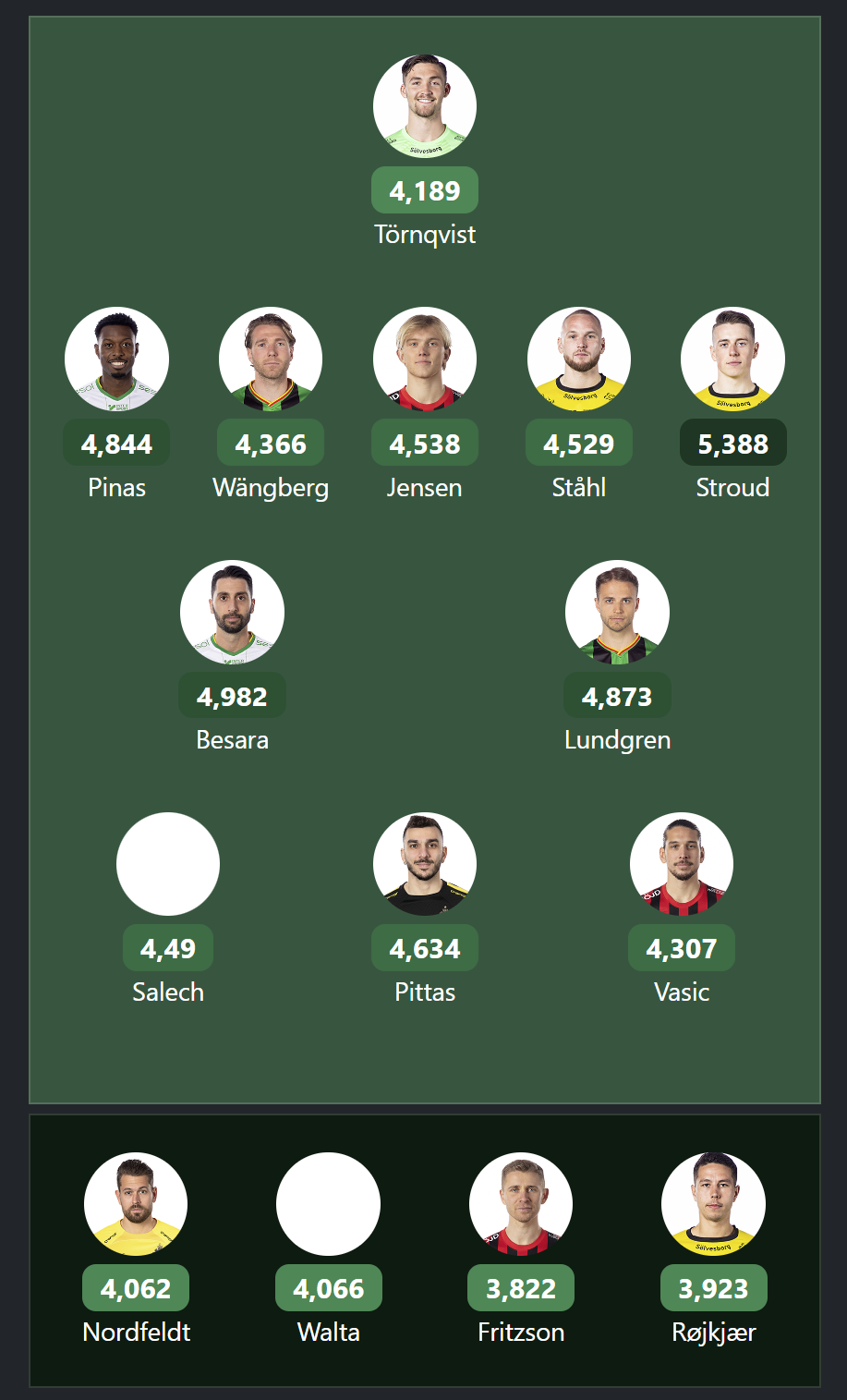
6. Key Takeaways

• Google OR-Tools is a powerful solver even in .NET environments.
• Modeling the problem correctly is more important than complex code.
• Optimization tools can bring real value to data-driven applications.

Feel free to reach out if you’re curious or building something similar!

---

✍️ Written by Viktor Nilsson, developer and fantasy football enthusiast.

📬 Follow me on LinkedIn for more .NET and football-related dev posts.